In a previous post, we looked at the design of my homemade gas pycnometer. For the past several months, I’ve been measuring the weight and volume of the whole and ground beans for my morning coffee. In this post, I’d like to look at some of those measurements, and then we’ll dig a little deeper into ground coffee density.
As usual, raw data and additional analysis are available on GitHub.
Overview
Let’s start with the big picture. The following plot shows density measurements for a range of coffees. These are sorted by whole bean density, but in practice this seems to correlate well with roast level, so roughly speaking we have dark roasts on the left and light roasts on the right.
Each point represents a single bag of coffee. The error bars show 95% confidence intervals based on the variance of individual measurements.

The whole bean and ground density measurements are particle density. These measurements include the solid material and any internal voids, but not the space between particles.
Ground measurements shown here were all made with a burr spacing of 100 ± 20 µm. This is measured from burr touch, so it’s not quite the same thing as nominal particle size. Burrs often have outfalls which interrupt the edge of the burr, so nominal particle size is usually larger than the burr spacing.
The tamped density measurements are bulk density. These measurements include the whole volume of the tamped puck.
Ground coffee density
Let’s look at the change in ground coffee density with burr spacing. The plot below shows ground coffee density divided by bean density. This adjusts for the effect of whole bean density (a denser bean will generally give denser ground coffee), so the changes we see here are due only to grinding.

At first it may not strike you as odd that ground coffee is denser than whole beans—we might think of it as packing a little tighter. But these are particle density measurements, which don’t include the space between particles. Consider whether you would expect small steel balls to be denser than big steel balls. Both should have the same density, because both are made of steel.
So why is it different for coffee? There are three main factors that likely contribute to the increase in density at finer grind settings:
- Fines (A): These have no internal pores, so they increase the average particle density of the sample.
- Open pores (B): These pores have become part of the space between particles, so they no longer contribute to particle volume.
- Closed pores accessible to air (C): Some closed pores may be connected to the outside via a series of cracks or micropores through which air can pass. These also will not contribute to particle volume.
These three factors are illustrated below.

We can model this by thinking of each particle of ground coffee as having a thin permeable layer near its surface which contributes to the mass of the particle, but not its volume.

The nominal volume of the particle is given by:
![Rendered by QuickLaTeX.com \[V_0 = \frac{4}{3} \pi \left( \frac{d}{2} \right)^3\]](https://quantitativecafe.com/wp-content/ql-cache/quicklatex.com-e506c480339b98d5266d5148601a4ebf_l3.png)
But the adjusted volume is:
![Rendered by QuickLaTeX.com \[V = \frac{4}{3} \pi \left( \frac{d}{2}- a \right)^3\]](https://quantitativecafe.com/wp-content/ql-cache/quicklatex.com-0757800fc21a0b2d1808368b2d4c4683_l3.png)
So the adjusted density is given by:
![Rendered by QuickLaTeX.com \[\frac{\rho_g}{\rho_b} = \frac{m / V}{m / V_0} = \frac{V_0}{V} = \left( \frac{d/2}{d/2 - a} \right)^3 = \left( \frac{1}{1 - 2 a / d} \right)^3\]](https://quantitativecafe.com/wp-content/ql-cache/quicklatex.com-9dba8bb5e86acfb308b603f131d35eaf_l3.png)
When ![]() , we can simplify this:
, we can simplify this:
![]()
However, in the espresso range we are very close to this limit, so in general I will use the original form of this model.
We can estimate nominal particle size, ![]() , using a constant offset,
, using a constant offset, ![]() , from burr spacing,
, from burr spacing, ![]() , so that:
, so that:
![Rendered by QuickLaTeX.com \[\frac{\rho_g}{\rho_b} = \left( \frac{1}{1 - 2 a / (d' - \delta_\rho)} \right)^3\]](https://quantitativecafe.com/wp-content/ql-cache/quicklatex.com-95d6931b0ef21eadbd162af49d1b79d0_l3.png)
Fitting the measured densities with this model, we get the following results:
Eureka Mignon Specialita (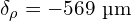 )
)

Timemore Sculptor 078S (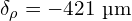 )
)

1Zpresso J-Ultra (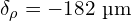 )
)

Interestingly, if we plot ![]() vs. whole bean specific volume, there is quite a good fit:
vs. whole bean specific volume, there is quite a good fit:

This suggests that we can estimate ground coffee density from whole bean density, burr spacing, and the burr spacing offset for each grinder.
Tamped density
To measure tamped volume, we start with the basket volume, measured by filling it with water. Then we subtract the volume of a cylinder whose top is the top of the basket, whose bottom is the top of the puck, and whose diameter is the inner diameter of the basket. The height of this cylinder can be measured using a digital caliper as described in my very first post.
Using ground density and tamped density, we can calculate void ratio as follows:
![]()
The following plots shows void ratio vs. burr spacing.
Eureka Mignon Specialita

Timemore Sculptor 078S

In these plots, hollow markers indicate a tamp using the Normcore V4 Tamper with 30 lbf spring, and solid markers indicate a force-controlled tamp of 15 kgf.
At coarse grind settings, void ratio appears to be nearly constant for each coffee. This suggests that for coarse grind settings, most of the variation in tamped puck density comes from changes in the density of the individual particles. I have approximated the constant void ratio using the 95th percentile for each plot, indicated with a dashed line in each plot.
At fine grind settings, void ratio falls below the dashed line, which is to say there is less empty space in the puck than expected. I suspect this results from the production of fines, which can fill the space between nominal particles. In the next post, we’ll look at a simple model of fines production, and we’ll see if we can fit this data using the model.
